5,. Indomable gravedad.

El campo gravitatorio […] tiene solo una existencia relativa. Porque si uno considera a un observador en caída libre, por ejemplo, desde el tejado de una casa, no existe para él campo gravitatorio durante su caída, al menos en su vecindad inmediata. La idea más feliz de su vida, de Albert Einstein.

En eso pensaba Einstein cuando, de repente, se sobresaltó porque había encontrado la forma de ampliar su relatividad especial a una forma general con aceleraciones. Ya sabía que las partículas muy rápidas multiplicaban su masa y su tiempo de vida como si fueran ajenas a nuestro sentido común, pero no sabía de qué forma funcionaría esa magia más allá de velocidades constantes. Ya son tantas y tan exactas las verificaciones de la relatividad general que negar su validez parece cosa de insensatos, pero no podemos ignorar que solo sirve a gran escala y no se comprende su relación con las partículas. Tampoco ayudan mucho los infinitos de la gravedad cuántica, ni las pruebas experimentales que no se pueden hacer con las teorías de cuerdas y de lazos, así que no es evidente que existan dueños del significado real de la gravedad. ¿Qué tal si revolvemos en algunos rincones donde jamás buscarían los mejores físicos del mundo?

La idea más feliz de su vida es una expresión en bruto del principio de equivalencia, y seguramente más fácil de comprender porque no tiene formalismos matemáticos. La clave para entenderlo es que no existe aceleración relativa entre objetos que caen juntos a muy corta distancia, lo que Einstein mencionó como “vecindad inmediata”. Como no existe aceleración en ese microentorno de gravedad, es posible aplicar leyes que se cumplan en ausencia de aceleraciones, como sucede con la relatividad especial. Así es como Einstein estableció una relación entre relatividad especial y gravedad, y así es como se convirtió en el primer interesado en que gravedad y aceleración fueran equivalentes a todos los efectos, lo necesitaba para seguir su camino en busca de una relatividad con aceleraciones.

La idea feliz nos dice que un observador en caída libre no es consciente del campo gravitatorio, y eso es como decir que no puede sentir su caída con velocidad creciente, es decir, con aceleración. Pero es falso, tendría que notar un aumento cada vez más rápido en el tamaño de la Tierra, o darse cuenta de que su camino se curva como evidencia de la gravedad. Einstein lo sabía y por eso matiza que será en su vecindad inmediata donde, al menos, no podría sentir la gravedad.

Un observador encerrado en su vecindad inmediata ya no sabría distinguir si flota en el espacio profundo, sin gravedad, o si tendrá tiempo para exhalar un suspiro antes de romperse la cabeza por culpa de la gravedad… ¿no es así? ¡Pues no!, el hecho de que la relatividad se aplique localmente no modifica la percepción de nadie, lo diga quien lo diga, así que hacen falta manipulaciones para convencer a un observador de que no puede distinguir la gravedad, ya sea con los ojos vendados, encerrado en una cámara sin ventanas, o cosas por el estilo. En su camino hacia la relatividad general, ¿para qué necesitaba Einstein observadores manipulados, y por qué los hizo desaparecer en la formulación definitiva de su principio de equivalencia? ¿Eran irrelevantes, o simplemente ponían en peligro su equivalencia?

Un observador encerrado en una cámara sin ventanas, manipulado, no podría distinguir si está en reposo sobre la Tierra o si está en el espacio dentro de un cohete acelerado, siempre y cuando acelere lo justo para que la fuerza de inercia (F) se iguale con su peso (P) sobre la Tierra. Si en esas condiciones también fueran iguales la masa gravitatoria (mg) y la masa inercial (mi), entonces tendría razón diciendo que aceleración (a) y gravedad (g) son lo mismo. El problema se traslada entonces a decidir si los dos tipos de masa son equivalentes a todos los efectos. Para los antiguos no eran lo mismo, pero Einstein ya sabía que las medidas experimentales apuntaban hacia una coincidencia completa, y así estableció con categoría de principio que los dos tipos de masa eran equivalentes. Así consideró que su camino estaba despejado para ir en busca de la relatividad general

La masa gravitatoria es la que siempre ha servido para medir cantidades de algo, y se mide con una balanza en reposo. La masa inercial es la que hace que algo tenga más o menos inercia, y se mide aplicando una fuerza y midiendo cómo frena o acelera. A pesar de la estricta coincidencia numérica, son tan diferentes en su medida y significado que parecen cobrar vida para gritar que NOOOO, que no son lo mismo. Es fácil comprender que cuesta poco atrapar una pelota de goma, y cuesta mucho detener un camión de 40 toneladas. Pues en el caso de que los dos tipos de masa fueran diferentes, las cosas ya no se comportarían exactamente como la pelota y el camión. No sabemos si algún día encontraremos la forma de reducir la inercia conservando la masa gravitatoria, pero ese sería el camino para poder llegar muy lejos en el Universo, un camino en el que dejamos de creer cuando Einstein convenció al mundo de que los dos tipos de masa eran lo mismo a todos los efectos.

Si gravedad y aceleración son lo mismo, entonces un cuerpo en reposo sobre la Tierra debería tener aceleración, a pesar de ser una magnitud que no tiene sentido sin movimiento. ¿Seguro que los dos tipos de masa son lo mismo a todos los efectos? Si las cargas eléctricas tuvieran aceleración en reposo, deberían emitir ondas electromagnéticas porque eso es lo que hacen las cargas aceleradas, deberían emitir energía sin consumir nada, y eso es evidente que no sucede. ¿Seguro que los dos tipos de masa son lo mismo a todos los efectos? Si la relatividad general nos dice que las curvaturas en las trayectorias de los cuerpos no se deben a una fuerza sino a que se ha curvado el espacio que recorren, entonces no deberíamos tener peso en reposo sobre la Tierra porque no recorremos ningún espacio. Si la teoría solo explica las trayectorias de caída libre pero no dice nada en condiciones de reposo, algo muy gordo debe de faltar en la teoría, porque nuestro peso en reposo también es un efecto de la gravedad ¿Seguro que los dos tipos de masa son lo mismo a todos los efectos?

La gravedad es la causa de que un cuerpo acelere si no hay nada que impida su movimiento, así que puede decirse que hay una relación directa entre aceleración y gravedad porque la masa es una constante. Pero la gravedad también es la causa de la presión contra el suelo que limita el movimiento, así que también puede decirse que hay una relación directa entre presión y gravedad porque la superficie de apoyo es una constante. ¿No es cierto que una hipótesis correcta se verifica en todos los casos posibles? Pues entonces aceleración y gravedad no son lo mismo porque no se verifica el caso de reposo.

Si la gravedad es una causa y aceleración solo es uno de sus posibles efectos, la igualdad entre gravedad y aceleración solo es matemática porque la causa y su efecto no son de la misma naturaleza, y si nosotros no somos conscientes de la diferencia entre la causa y el efecto, las matemáticas tampoco lo serán. Lo siento, mis ojos ven, y mis pies me dicen que se comprime la tierra que piso, distingo perfectamente que mi peso sobre la Tierra no es lo mismo que mi reacción contra el suelo de un cohete acelerado, son las matemáticas las que no pueden distinguir la diferencia. Lo siento y no lo siento, da igual, me parece que ya entiendo por qué desapareció el observador consciente del principio de equivalencia, y por qué se puso en su lugar un observador matemático.

Si fuera cierto que gravedad y aceleración son la misma magnitud física, un campo de gravedad tendría que ser un campo de aceleraciones, y cada punto localizado del espacio vacío, que no se mueve, debería tener aceleración como si fuera un objeto en movimiento. Es absurdo, muy, muy absurdo, pero al fin y al cabo es correcto para un observador con los ojos vendados o encerrado en una cámara sin ventanas. El observador de Einstein era matemático, ciego delante de la realidad pero eficiente cuando se trata de calcular, así que no parece imposible cosechar verificaciones numéricas a la vez que desencantos, porque nada se sostiene para un observador consciente de lo que hay más allá de su vecindad inmediata.

La gravedad puede ser lo que siempre nos había parecido, una especie de ligadura invisible y elástica que nos mantiene conectados a la Tierra. Sería la fuerza resultante de multiplicar la tensión y la sección de la ligadura, y sería la causa de acelerar un cuerpo alejado de la Tierra, de igual forma que las gomas de un tirachinas aceleran una piedra. ¿Y si estamos en reposo sobre la Tierra? Pues lo mismo, también será la causa de nuestro peso y de la reacción del suelo que limita nuestro movimiento. Por muy simple que parezca, la fuerza de una ligadura invisible y elástica puede ser la causa común del peso en reposo y del movimiento acelerado, condiciones que la relatividad general solo cumple a medias.

¿Cómo es posible que la materia pueda deformar el espacio-tiempo a distancia si no se reconoce ninguna continuidad entre materia y espacio vacío? Lo que se ha llamado espacio-tiempo debe ser una extensión real de la materia que se debería tensar hasta la superposición con otra extensión, de otro cuerpo, y esto enlaza con el capítulo anterior titulado La sinfonía inacabada del Universo, donde poníamos a prueba un posible mecanismo de propagación de la luz sin paradojas entre ondas y partículas.

La radiación sobrante del Sol debería expandirse y ocupar capas muy externas de su campo estacionario, y si el campo terrestre se tensa y conecta con el campo solar en lo que podemos llamar superficie de enlace (Se), entonces la radiación invadirá el campo terrestre proyectándose como partículas localizadas y completas, ya que cada onda convergente concentrará puntualmente toda su energía. Si el campo terrestre se tensa como una ligadura elástica, debería propagar ondas transversales de forma similar a lo que sucede con una cuerda tensada, y esas ondas transversales tienen que ser lo que llamamos luz. Por lo tanto, el mismo mecanismo de propagación de la luz también será responsable de la gravedad si el modelo es acertado, y sobre todo, habríamos encontrado una conexión entre la gravedad y las partículas, ya que muchos campos elementales en superposición formarán otros campos a mayor escala de integración, como el caso del Sol y la Tierra.

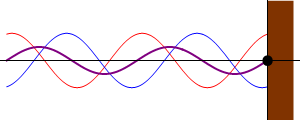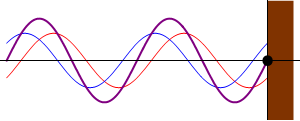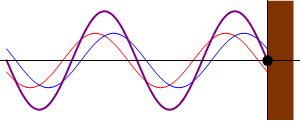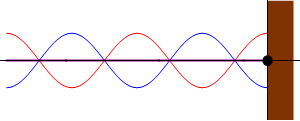
La superficie de enlace (Se) será entonces una superficie compartida, y en ella tendrán lugar las acciones que cada campo ejerce sobre el otro, de forma similar al empuje de un fluido a presión sobre una superficie. Cuanto mayor sea el número de partículas más denso será el campo resultante, mayor será la presión sobre la superficie compartida, y mayores las acciones transferidas al otro campo. En la imagen vemos un ejemplo de 2 y 3 partículas de color azul y rojo, donde se han dibujado las fuerzas o acciones aplicadas al campo rojo. La desviación del grupo azul hacia la izquierda tensará su campo con resultante hacia la izquierda tirando del campo rojo, cuya reacción de inercia se ha dibujado en rojo.

Si la gravedad se debe a que los campos de materia se tensan, es evidente que su efecto puede ser aceleración o reacción contra lo que impida el movimiento, como los pesos en la Tierra, y también es evidente que gravedad es una causa de aceleraciones, pero no es aceleración.

Como las acciones o fuerzas aplicadas en la superficie de enlace tendrán resultante en una sola dirección, lo podemos comparar con cables tensados que unen a los dos cuerpos en su centro de masas C. Es cierto que la sección de un cable será la suma de secciones de todos los hilos que lo forman, pero en el caso de partículas debemos entender que su geometría no es lineal sino esférica, que comparten la misma superficie de enlace, y que al añadir más partículas no aumentamos la superficie que cubren sino que hacemos más denso el campo en esa superficie. Como la geometría esférica es más difícil de imaginar, vamos a cambiar partículas por hilos en tensión y masas por cables de muchos hilos, conectados en una sección común (Se) y coincidente con el centro de masas (C).

El número de hilos de cada “cable” o campo, tiene que ser equivalente a lo que llamamos masa gravitatoria porque se corresponde con el número de partículas, pero siempre se pueden definir unas condiciones normalizadas en las que masa gravitatoria y peso coinciden, solo hay que recordar que así es en cualquier lugar de la Tierra en el nivel del mar. Es correcta la equivalencia entre número de hilos y masa, pero también se puede hablar del número de hilos como de la fuerza que puede hacer un campo en unas condiciones determinadas, y la densidad será entonces como la tensión de un cable o la presión de un fluido. No se pueden comparar los dos campos con diferentes números de hilos, y tampoco son iguales las densidades, pero se pueden determinar las secciones equivalentes de forma que las densidades valgan 1 en los dos campos. En esas condiciones, la fuerza o acción de A sobre B (Fab), será como la presión (densidad) del campo A (Da) por la superficie equivalente de B (Sb). Así se comprueba que la fuerza o acción de B sobre A (Fba) es igual que la de A sobre B, como debe ser para el equilibrio.

¿Conclusión? Pues que la fuerza de gravedad es completamente igual que la de Newton si radio de enlace (Re) y distancia (d) son proporcionales. No es una fórmula experimental porque se ha deducido de un modelo previo, y si ponemos atención a las unidades comprobamos que son coherentes, no aparece ninguna constante con unidades como pasa con G en la fórmula de Newton. Sin embargo es cierto que faltaría por determinar la proporción entre radio de enlace y distancia, y la relación entre los números de hilos o partículas con las masas. Donde Newton ponía masas, nosotros también podemos poner superficies esféricas que contienen a los cuerpos afectados por la gravedad.

La superficie de enlace tiene que tener un máximo en la densidad porque es ahí donde dos campos entran en superposición. Esa capa de mayor densidad será entonces como una superficie parcialmente reflectante, un medio de conexión entre dos cuerpos que interaccionan con ondas de ida y retorno. Átomos, cuerpos macroscópicos, planetas, estrellas…, da igual, todo puede estar hecho de campos estacionarios que limitan su expansión mediante superficies de enlace más densas, a lo largo de una interminable jerarquía de escalas de integración. De alguna forma, la información contenida en una superficie de enlace representa todo lo que contiene dentro, exactamente como los físicos Leonard Susskind y Juan Maldacena derivaron de la teoría de cuerdas, denominado “principio hologrático”. Es evidente que un campo estacionario tiene propiedades holográficas, pero habrá que dejar ese tema para más adelante.

Ya se ha demostrado que al añadir un retardo de transporte en la gravedad de Newton se predicen las variaciones correctas en la órbita de Mercurio, las mismas que predice la relatividad general. Lo que pasa es que la gravedad de Newton no tiene soporte teórico para justificar un retardo de transporte, pero la superposición de campos que se ha descrito sí lo tiene, ya que la superficie de enlace sería como una cámara de resonancia en la que rebotarían verdaderos ecos de gravedad, un retardo de ida y vuelta como se necesita realmente para explicar las anomalías en la órbita de Mercurio.

También se puede adelantar una pequeña mención a la estabilidad orbital. La fórmula de Newton no puede dar cuenta de ninguna clase de correcciones en la excentricidad de las órbitas, y mucho me temo que la relatividad general tampoco, a menos que algún genio de las ecuaciones diferenciales lo demuestre con las ecuaciones de Einstein. Sin embargo el modelo de campos estacionarios establece una realimentación entre los cuerpos y la superficie de enlace. El radio de esa superficie debería tender a ser proporcional a la distancia, pero sus correcciones llegarán siempre con retraso y eso tendrá un efecto que corrige lentamente la excentricidad orbital, ya veremos que es cierto, pero ahora no podemos extendernos y vamos a limitarnos a dejar en el aire una pregunta: Si dibujamos a escala las órbitas reales de los 8 planetas del sistema solar, hasta la de Mercurio parece casi un círculo perfecto, siendo la más excéntrica. ¿De verdad tuvimos tanta suerte que todos los planetas acertaron por casualidad a seguir una órbita perfecta? ¿A pesar de los terribles cataclismos que suponemos en su formación?

Siento que no haya sabido explicar el problema sin algunos tecnicismos, pero creo que todo lo dicho es estrictamente correcto, que no hay duda, y que va siendo hora de pensar en una gravedad sencilla por mucho que le pese a la relatividad general y a la mecánica cuántica. Es hora de reescribir la historia de la realidad.

Principio de equivalencia (Albert Einstein).

En cada punto del espacio-tiempo en el que exista un campo gravitatorio arbitrario, función continua de puntos, es posible siempre escoger un sistema de coordenadas localmente inercial tal que, en un entorno suficientemente pequeño del punto, las leyes de la naturaleza toman la misma forma que en los sistemas inerciales de la relatividad especial en ausencia de fuerzas gravitatorias.

Anterior              Siguiente

4.- La sinfonía inacabada del Universo.

Después de tantos éxitos y reconocimientos cosechados por Einstein, el mundo se despertaba cada mañana esperando encontrar en primera página una perfecta y definitiva sinfonía del Universo. Algo hay en lo profundo de la materia que oscila y resuena como las notas puras de un instrumento musical, pues no en vano los electrones ocupan solamente determinados niveles de energía que corresponden a notas puras, como cuerdas bien afinadas que solo pueden vibrar en determinadas frecuencias de resonancia.

Hace ya un siglo que se publicó por primera vez una extrañísima interpretación de la gravedad y el Universo a gran escala. La teoría de la relatividad general que Albert Einstein sacó a la luz en 1915 nos habla de un entramado en el que tiempo y espacio no se pueden separar, un entramado que se tensa y se curva en función de la materia presente, pero sin relación alguna con el mundo de las partículas. Como ya se conocía la relación entre fuerzas nucleares y electromagnetismo, solo faltaba relacionar electromagnetismo y gravedad para conectar a todas las interacciones conocidas, algo así como la última frontera de la física.

Buscar esa relación era como buscar una teoría del todo, y así pasaban los años compartiendo disputas con una floreciente mecánica cuántica que también pujaba por hacerse dueña del todo, intentando demostrar que ya era una teoría completa y que la gravedad tenía que deducirse como una consecuencia natural de sus postulados. Einstein, a punto ya de morir, todavía encontraba fuerzas para negar a la mecánica cuántica sus pretensiones de ser una teoría completa, diciendo que nadie sabía lo que de verdad era un fotón. Einstein murió en 1955 dejando el monopolio a la mecánica cuántica, ¿no va siendo hora de preguntarse si por fin se ha ganado la reputación de ser una teoría completa del todo?

La teoría cuántica de campos trata el vacío como una fuente inagotable de energía que crea y aniquila partículas como una distribución estadística. Donde la probabilidad es alta, las partículas tienen mayor estabilidad y es donde supuestamente aparecen los átomos, moléculas, y todo tipo de agrupaciones que llamamos materia. Mucho se habla de la teoría cuántica de campos como la más precisa de la historia, sin embargo apenas existen divulgadores que nos cuenten los problemas que todavía no ha superado, ni puede superar.

Para que una función tenga en cuenta los efectos relativistas tiene que definirse localmente, pero los operadores de la teoría cuántica de campos no son funciones sino distribuciones estadísticas, y no tienen sentido en intervalos infinitesimales como exige una verdadera definición local. No es de extrañar que aparezcan divergencias infinitas debido a un formalismo matemático tan espinoso, parcheado con un proceso de “renormalización” que se come los infinitos mediante grados de libertad con dudoso significado físico. Dirac, el físico y matemático que predijo la existencia de antimateria, y uno de los desarrolladores de la teoría cuántica de campos, terminó afirmando que la teoría de renormalización había salido victoriosa de todos los intentos para sanearla de modo matemático. Una descripción detallada la podemos ver en el siguiente documento de un profesor de la Universidad de Elche, aunque difícil de seguir por sus complicados conceptos de matemáticas.

Cada tipo de partícula tiene su propio campo cuántico, y si hablamos de gravedad cuántica debería existir una partícula que se ha llamado “gravitón”, hace ya mucho tiempo, pero resulta que sus infinitos no se pueden “renormalizar” y la gravedad se queda fuera de las pretensiones de la teoría cuántica de campos. Más de 60 años después del desarrollo de la teoría, no solo no se ha conseguido la deseada unificación con la gravedad sino que ni siquiera se puede asegurar que sea estrictamente compatible con la relatividad especial.

Cuando hablamos de compuestos químicos, la teoría cuántica se aplica con tal número de simplificaciones que se hace difícil esperar predicciones acertadas. Es tan complicada que a duras penas vislumbra los orbitales de un solo electrón en un átomo de hidrógeno, y esto no es algo que se predique mucho por ahí, pero es cierto, así que podemos decir que las partículas mejor investigadas en el dominio cuántico son dos: Un protón, y un electrón solitario jugando a los dados en sus proximidades.

Sí, Einstein murió en 1955, y podemos asegurar que 60 años después todavía no sabemos lo que de verdad es un fotón y solo podemos hablar del Universo como de una maravillosa sinfonía, pero inacabada. Es increíble que después de tanta relatividad y tanta mecánica cuántica, no alcancemos a imaginar a la materia más allá de una impresión artística, así que vamos a reunir lo poquito que sabemos y añadir lo que podemos imaginar, sabiendo perfectamente que nos enfrentamos a una forma de pensar especializada en cosechar éxitos, mientras pasa por alto que no sabe lo que de verdad es un fotón. Si de verdad queremos entender a la materia, ¿hay algo de realismo que merezca salvarse de la hoguera cuántica?

Alguna vez habrás jugado con una cuerda, habrás visto la magia del contoneo que la recorre cuando aplicas un pulso en uno de sus extremos, y también habrás visto que serpentea cuando agitas el extremo con frenesí. Ya entiendes entonces que al obligar a oscilar a un medio físico, como una cuerda, la oscilación se propaga por el medio en forma de ondas, ya entiendes que una onda no es una “cosa” porque la realidad física no está en la onda sino en el medio que la propaga. Bueno, no para todo el mundo es así, muchos físicos todavía piensan que la luz es una onda sin medio porque nadie ha sabido entender que hay algo real escondido en el vacío, es más fácil seguir el atajo de una función experimental sin cimientos de realidad.

Es posible que alguna vez hayas aplicado un pulso con un extremo de la cuerda sujeto en un punto fijo, y habrás visto que cuando alcanza el extremo fijo se invierte y rebota. La forma del pulso durante la transición coincide con la suma de dos pulsos iguales e invertidos que se propagan en sentidos opuestos. Si la cuerda se fija en los dos extremos, el pulso no dejará de invertirse y rebotar en ambos lados hasta que la energía se pierda en forma de calor.

¿Y si en lugar de un pulso se propaga una onda completa? También se invertirá y rebotará, pero como una onda invertida es igual que la onda original, entonces la onda incidente y la reflejada son iguales pero se propagan en sentidos contrarios, y la suma de ambas da como resultado una onda muy extraña, llamada onda estacionaria porque no se propaga. En realidad se trata de un estado de vibración de la cuerda que produce un sonido audible si la frecuencia está comprendida entre 20 y 20000 oscilaciones por segundo, supuestamente los límites de nuestra percepción. No te pierdas las siguientes animaciones de ondas ni dejes de ver alguno de los vídeos incluidos, el primero especialmente, y si no simpatizas mucho con las matemáticas no pasa nada si te saltas esa parte del vídeo.

Alguna vez habrás montado en un columpio y habrás aprendido a voltear el cuerpo hacia atrás cuando avanzas, y adelante cuando retrocedes. Ya sabes que las oscilaciones aumentan cuando aplicas energía en los momentos justos y en el sentido correcto, sabes perfectamente que la frecuencia de tus impulsos y la frecuencia de oscilación del columpio tienen que ser iguales, porque si te desfasas te frenas. Sin matemáticas y sin conocimientos de física ni de ingeniería, ya entiendes cómo se debe regular un proceso para que oscile o para que se detenga. Todo lo que puede oscilar tiene una o varias frecuencias naturales que determinan la forma en que interacciona con el resto de las cosas. Tu columpio favorito también tenía una frecuencia natural, y tenías que aprender a tantear esa frecuencia para conseguir dominarlo. ¿Sabías que al igualar la frecuencia de tus impulsos con la frecuencia natural del columpio, experimentabas una “resonancia” porque “sintonizabas con el columpio”?

Cuando de repente se amplifica una oscilación es porque ha sintonizado con alguna fuente de energía. La cuerda que vibra con más amplitud, el sonido que se hace más fuerte, las microondas que achicharran la comida, el puente que oscila y se derrumba, la radio que de repente sintoniza una emisora, la mano temblorosa de un enfermo de parkinson, el columpio que te acerca hasta el cielo impulsado por tu vitalidad… son algunos ejemplos de resonancia en los que toda onda se transforma en oscilación estacionaria, en vibración que no se propaga. Las ondas estacionarias vienen siempre acompañadas de resonancia porque las ondas incidente y reflejada no se desfasan respecto de la oscilación del medio, y eso se cumple cuando el número de semiciclos entre los extremos es entero. Ese número de semiciclos depende de la rigidez o tensión del medio, y de la frecuencia, por eso se afina una guitarra tensando sus cuerdas hasta distinguir las notas puras por un sonido más intenso y prolongado.

La imagen anterior demuestra la resonancia en una cuerda que oscila de forma estacionaria, pues vemos claramente una onda de mayor amplitud que también se mantiene más tiempo cuando deja de recibir energía. Si las pérdidas fueran cero, la energía se conservaría y nunca dejaría de oscilar. No se conoce nada que oscile sin pérdidas en el mundo que vemos y tocamos, pero los electrones lo hacen en todo momento como si estuvieran enclavados en alguna de sus frecuencias naturales de oscilación, y cuando alguna perturbación destruye su resonancia y los arranca de su escondite, vuelven a caer en otra de sus frecuencias naturales con su nivel correspondiente de energía. Los niveles de energía de los electrones coinciden con modos de oscilación estacionaria de un número entero de semiciclos, y ese número entero es justo el número cuántico principal de su función de onda.

Efectivamente, un electrón no puede perder o ganar energía en cualquier cantidad, solo pierde o gana la diferencia entre su nivel y otro nivel inferior o superior, que también será un estado de resonancia. Esa diferencia es precisamente la energía que se va en forma de fotón, o la que absorbe en forma de fotón. Por lo tanto, al descomponer la luz emitida o absorbida por los diferentes elementos químicos, solamente deberían verse determinadas frecuencias y quedar desiertas todas las intermedias. Eso es justo lo que se ve, y es la prueba de que los electrones ocupan estados o niveles de resonancia como las ondas estacionarias. De alguna forma, cada electrón debe ser algo que oscila entre los límites de un átomo, lo mismo que una cuerda oscila entre los extremos fijos que limitan la propagación de sus ondas. ¿Y qué clase de medio será un electrón, qué clase de oscilaciones propaga, y qué clase de límites imponen los átomos para contener su propagación? Ecos, ecos de realidad golpean a las puertas de la mecánica cuántica, y con impaciencia me pregunto cuál será su respuesta…

El número entero de semiciclos que hacen falta para que las oscilaciones de “algo” se hagan estacionarias, es el número cuántico principal que alcanza el recibidor de la función de onda, el último rastro de realidad que se pierde definitivamente para dejar paso al retorcido y psicodélico espacio de Hilbert, donde solamente oscilan probabilidades… ¡Qué desperdicio!, toda la física cuántica del mundo no sirve a partir de ahí para seguir buscando lo que de verdad oscila y resuena, así que aquí se termina la poquita realidad que se puede salvar, y aquí comienza lo que se puede imaginar.

Me arriesgo, nunca dejaré de creer que la realidad física está en el medio y no en la onda que se propaga, y si un electrón se comporta como un perfecto medio de oscilación, debe de ser porque lo es. Si la energía de la luz es la misma que pierden o ganan los electrones cuando cambian su modo de oscilación, debe de ser porque la luz no es más que la onda que se propaga y los electrones son el medio, así que no es imposible deducir el aspecto de un electrón aunque no podamos verlo, porque si somos capaces de seguir a las ondas de luz en el espacio, estaremos siguiendo la forma del medio que las propaga. ¿Cuál es entonces la forma de las ondas de la luz?, ¿cuál es?

Si ponemos una fuente de luz y una segunda fuente idéntica pero doblando la distancia, observamos a la segunda con una intensidad cuatro veces menor, no igual ni la mitad. Eso nos dice que la luz no se comporta como las ondas en una cuerda, pues entonces no habría pérdida de amplitud y las dos luces deberían verse con la misma intensidad. Tampoco se comporta como las ondas planas en la superficie del agua, pues entonces el contorno circular de cada onda se duplicaría si también se duplica su radio, y como la energía de la onda debe repartirse por toda la onda, la intensidad observada debería ser la mitad, no 4 veces menor. Definitivamente, la luz está relacionada con ondas esféricas cuya superficie aumenta con el cuadrado de su radio, y si repartimos la energía por toda la onda, duplicando el radio, entonces la intensidad se reducirá 4 veces como se demuestra en la práctica.

La forma de un electrón tiene que ser esférica, y su extensión en el espacio debería superponerse con la de toda la materia hasta llegar tan lejos como alcance la luz, así debe ser si la realidad física está en el medio y no en la onda, porque ya no habrá onda donde su medio no alcance. Si el famoso entramado de tiempo y espacio no es más que la extensión ondulatoria y estacionaria de la materia, de repente se comprende por qué se deforma el espacio-tiempo y de qué forma se relaciona con las partículas de materia. Pero si esa extensión no se ve, ¿cómo se puede pensar que existe? Tampoco se puede ver el espacio-tiempo ni los campos cuánticos, y ahí están, llenándonos la cabeza de paradojas.

Sabemos que la luz está dividida en pequeños paquetes de energía que denominamos fotones, y dichos fotones no se dividen jamás. Así lo demuestra el efecto fotoeléctrico, el efecto Compton, y la creación de pares de partículas que pueden ser creadas con dos fotones pero nunca con uno solo. Es evidente que una radiación se reparte por igual en todas direcciones manteniendo siempre fotones completos. Cada fotón que alcance a una de nuestras retinas llegará siempre completo sin que importe la distancia. Un fotón de alta energía es igual de peligroso para nuestros ojos cuando es emitido a escasos centímetros que cuando es emitido desde el Sol.

Bien, se podría decir que una radiación es en realidad como una lluvia de partículas en todas direcciones, pero eso tampoco es cierto porque diferentes experimentos de difracción demuestran patrones ondulatorios incluso emitiendo partículas de una en una. Si cada fotón por separado es una onda esférica que se desparrama en todas direcciones, ¿cómo puede llegar completo puntualmente a un determinado lugar? Argumentos como ese los encontramos en cada libro de iniciación a la física cuántica, condiciones imposibles que según los autores deberían dejarnos claro que no vale la pena intentar comprenderlo. De alguna forma nos dicen que la razón ha muerto pero que no pasa nada… ¿¡Cómo qué no pasa nada!? ¿Por qué no vale la pena comprender todo lo que pone en peligro a la versión probabilística de la función de onda?

Si cada partícula es un medio que oscila de forma estacionaria y su geometría es esférica, una sección plana revelaría capas concéntricas que nos recordarían a las ondas en el agua, aunque oscilando sin propagación. La siguiente animación de ondas estacionarias planas puede ayudar a entender mejor el concepto, ya que resulta imposible dibujar y animar en tres dimensiones lo que podemos llamar un campo de ondas estacionarias de geometría esférica.

Cuando ese campo de ondas estacionarias cambie su modo de vibración a otro de menor energía, la energía sobrante será expulsada hacia el exterior en forma de ondas esféricas. Un electrón, un átomo, una molécula, cualquier objeto radiante, es el evidente medio en el que se propagan esas ondas que denominamos fotones de luz, y si entendemos que se libera de lo que le sobra expandiéndolo, ¿de qué forma debería capturar energía cuando le falte?... ¿No se entiende que debe hacerlo igual pero en sentido contrario?

Piensa en el Sol, rebosando energía que debe retirar hacia capas más y más externas de su campo estacionario. Esa energía tocará la Tierra y formará un mar de interferencias con el campo estacionario terrestre, pero las interferencias no pueden ser la vía de transferencia de la luz… ¿Por qué? Pues porque cada fotón será una onda esférica completa y en su interferencia cedería solo una minúscula parte de su energía, inversamente proporcionar al cuadrado de la distancia como corresponde a las ondas esféricas, ¿se recuerda?... Entonces… ¿Qué? Pues que la radiación solar se acabará expandiendo lo necesario hasta conectar completamente con el campo terrestre, ondas completas con ondas completas, y entonces el campo terrestre se irá llenando de radiación convergente, dibujando la pequeña realidad que observamos como fina lluvia de partículas de luz.

            ¿No explica eso por qué un fotón se libera como una onda en expansión pero es capturado como partícula? Las capas más externas de un átomo excitado son el cuarto donde acumula lo que le sobra, y esas mismas capas de otro átomo más frío son el recibidor de lo que le falta. Si los dos átomos comparten esas capas en el espacio como si fueran un solo átomo, entonces el más frío captará el fotón en forma de ondas convergentes, completas, nunca en forma de interferencias con ondas en expansión, porque la energía que pueden entregar disminuye demasiado rápido con la distancia.

            Enhorabuena si lo entiendes, porque así de simple puede ser la solución a los 100 años de paradoja onda-partícula, ese virus de ignorancia que mató el sentido de la realidad a los físicos más influyentes de nuestra historia reciente, es tan simple que parece mentira si no ponemos en ello toda la razón, todo el corazón, y todo el alma. Ecos de realidad golpean cada vez más fuerte a las puertas de nuestra ciencia, pero aquellos que deciden qué es la ciencia no dejan de poner contrafuertes y se agota la esperanza de apertura, ¿hasta cuándo resistirá su fortaleza sin cimientos de realidad?

Anterior         Siguiente

Ondas estacionarias panas.

Si llenamos de agua un recipiente circular y provocamos oscilaciones en el centro, produciremos ondas que se expanden hasta rebotar en el contorno del recipiente. Las ondas reflejadas se propagan entonces hacia el centro del recipiente y se suman a las ondas incidentes.

 

La suma o superposición dará lugar a oscilaciones estacionarias planas y concéntricas, un modo de vibración de la superficie del agua como el que vemos a continuación:

Realmente, la intensidad o amplitud debería disminuir al aumentar el radio, ya que la energía de cada onda debe repartirse sobre un perímetro que aumenta. El resultado es más o menos el siguiente:

Si la magnitud que oscila no es un desplazamiento como sucedería con cada molécula de agua, las variaciones de amplitud podrían representarse mediante cambios de color. Algo así ocurriría con las ondas de sonido si representamos los cambios en la densidad del medio:

Animación de ondas.

Propagación de un pulso aplicado en uno de los extremos de una cuerda:

Si repetimos los pulsos en pequeños intervalos de tiempo se propagan ondas completas:

Propagación de un pulso con el extremo fijo de la cuerda:

Fijando los dos extremos y suponiendo que la energía no se pierde, el pulso recorrería la cuerda ininterrumpidamente.

Formación de una onda estacionaria:

Experimento de ondas estacionarias en una cuerda (universidad de Alicante):

Experimento de ondas estacionarias en el agua:

Placa oscilando de forma estacionaria con arena que se concentra donde no hay oscilación, lo que podemos denominar líneas nodales.

Ondas estacionarias en una pompa de jabón:

Ondas estacionarias de sonido. El nivel sonoro dentro del tubo se intensifica cada vez que la longitud que recorre el sonido dentro del tubo es múltiplo exacto de media longitud de onda.

Ondas circulares y estacionarias en la superficie del agua. El experimento permite medir la velocidad de las ondas en la superficie del agua.

Ondas estacionarias en un muelle.

Las ondas estacionarias del sonido son la clave para medir su velocidad del sonido.

Y sucede lo mismo si en lugar de sonido es radiación electromagnética como la luz. Un simple microondas puede servir para medir aproximadamente la velocidad de la luz.

Experimento de ondas estacionarias en una onda plana, similar a la superficie de un puente:

El puente de Tacoma se destruyó porque se puso a oscilar de forma estacionaria.

3.- En el otro lado de la realidad.

El Universo, la Tierra, la casa que habitamos… ¿Quién pensaría que no existen? Decimos que son reales porque sí, porque los vemos a ellos y a las partes en que se dividen. Existen los ladrillos de nuestra casa y el cemento que los mantiene unidos, pero la física nos está diciendo que la división en partes tiene un límite, y al atravesarlo desaparece la realidad subjetiva que tiempo atrás no hacía falta definir con precisión. Ahora la realidad macroscópica no se puede entender de la misma forma que los estados de una partícula, hay categorías de realidad, mucha incertidumbre, y mucha expectación por descubrir a dónde conduce el laberinto de la razón.

Quizás estaremos de acuerdo en que “realidad” es el conjunto de todo lo que existe, pero decidir qué existe y en qué condiciones no es tan fácil como parece. Quizás estaremos de acuerdo en que realidad y materia se dan estrechamente la mano, así que vamos a investigar si las evidencias experimentales nos hablan fuerte y claro sobre una inquietud que nos pertenece a todos, comenzando con el viejo problema de medir magnitudes como longitud, tiempo y masa.

La falta de precisión en la medida siempre ha bloqueado el avance de la ciencia porque las teorías que no se pueden falsear se quedan en un limbo metafísico y no se desarrollan. Por ejemplo la supervivencia de la relatividad general de Einstein dependía de cuánto se desviaba la órbita de Mercurio, una variación angular tan pequeña que para medir una desviación de un solo grado necesitaríamos esperar 8372 años, eso es el equivalente a los famosos 43 segundos de arco por siglo que Einstein acertó a calcular con su propia teoría, y eso fue lo que se midió.

Se diría que alguna vez tendríamos que alcanzar la precisión absoluta, y entonces, por fin, quedarían al descubierto los secretos mejor guardados de la materia, una realidad tan objetiva y predecible como imaginaba Laplace en su “mecánica celeste”. Sin embargo, al dividir y dividir a la materia hasta llegar al submundo de las partículas, resulta que los fotones de la luz que se necesitan para “ver”, para medir, transportan tanta energía que al incidir sobre la partícula observada la sacan de cualquier límite de observación, y adiós medida.

Hay un límite allá en lo muy pequeño donde la precisión de medida se vuelve divergente y la realidad predecible se disuelve como si todo estuviera dominado por el caos. Pero si de verdad es el caos lo que domina la materia en su escala fundamental, ¿cómo es posible que surjan macrosistemas tan ordenados y coherentes como los seres vivos? ¿El orden puede surgir de un caos elemental, como si las partículas fueran piezas de un puzzle que se juntan correctamente por casualidad?

           No existe ninguna tecnología de precisión en el mundo de las partículas y eso basta para cuestionar lo que siempre se había pensado de la realidad, pero el problema de la medida no se debe solamente a los errores propios de la tecnología, es que verdaderamente las partículas tienen una existencia indeterminada. Eso significa que no hay ninguna garantía de que sigan trayectorias continuas, porque ni siquiera se puede afirmar que existen en cualquier instante del tiempo.

            Tal como sabemos por la física cuántica, el principio de indeterminación de Heisenberg está verificado experimentalmente, y nos dice que al multiplicar los errores de medida de dos magnitudes complementarias el resultado es una constante. Así por ejemplo si reducimos a cero el error de velocidad, entonces el error de posición se hace infinito y la partícula podría estar lo mismo aquí como en cualquier otro lugar del Universo. También es correcto decir que si una partícula virtual se desintegra en un tiempo muy pequeño, entonces tendrá una masa enorme. Por ejemplo el bosón W, una partícula que surge de la desintegración de un solo neutrón, es tan pesada como un átomo de hierro completo y eso incumple todos los principios de conservación de masa y energía. Una energía descomunal se oculta en el vacío más absoluto, y por alguna razón que nadie comprende, a veces presta un poco de su energía con la condición de que sea devuelta, a veces crea un “trocito de realidad” completamente nuevo a cambio de que solo exista durante un instante.

Muy bien, ya sabemos que por mucho que se afine la medida de magnitudes físicas, nunca servirán para darnos una imagen clara de la realidad primitiva que lo gobierna todo, son meros condicionantes históricos y culturales que reflejan la forma en que los antiguos humanos “pensaban” la realidad. Si las magnitudes como longitud, masa y tiempo son tan viejas como sabemos, y es evidente que los antiguos humanos no acertaron ni de lejos a describir lo que ahora sabemos de la materia, ¿no es evidente que si ha cambiado la forma de pensar la realidad, también deberían cambiar las magnitudes con que se mide?

             No me extrañan en absoluto las incontables paradojas que arrastra la física moderna, ni los casi ridículos parches con los que se tapan tantos agujeros de ignorancia. Defendemos que la ciencia es inflexible y rigurosa… ¿utilizando magnitudes que se derriten como la mantequilla? Por muy avanzada que sea la tecnología del metro, del kilogramo y del segundo, nada sirve para medir algo que puede ocultarse en el vacío y aparecer en otra posición y en otro tiempo. Definitivamente, la realidad no es algo que se divide hasta llegar a unos trocitos indivisibles, es algo que se funde con el vacío cuando parece que estamos cerca de alcanzar esos trocitos indivisibles, que no existen.

            El problema de la medida es desconcertante pero el experimento del que hablaremos ahora es, a juicio de muchos, la implicación más profunda de la física. Si tuviera que mencionar solo tres verdades universales no tendría duda en decir que la Tierra no es plana, que la Tierra no es el centro del Universo, y que la realidad es una telaraña de vínculos no locales que interconectan todo. John S. Bell publicó en 1964 un texto que pronto se conocería como el teorema de Bell, o desigualdades de Bell, y Alain Aspect, en su tesis doctoral de 1983, describió por primera vez un experimento que haría posible su verificación. Unos años más tarde se realizó con éxito el experimento y desde entonces ya sabemos que un principio de no localidad ha marcado para siempre a lo que llamamos realidad.

Todo comenzó al comprobar que la luz se podía comportar como partículas y que las partículas se podían comportar como las ondas, siendo Einstein el primero en acuñar el concepto de la “dualidad onda-corpúsculo” como dos formas diferentes de ver una misma realidad. No comprendía el por qué de tan extrañas manifestaciones de la luz y la materia, pero creía en causas ocultas que algún día se revelarían evidentes.

           Por muy extraño que resulte, la luz y la materia responden a probabilidades que se propagan como las ondas, se difractan y se interfieren, se suman y se complementan como si fueran dos partes en que se divide la nada. Allí donde la probabilidad es alta, una masa puntual aparece y reacciona como si fuera un proyectil, y si dos posiciones que distan años luz tienen alguna probabilidad asociada, en cualquiera de las dos puede aparecer la partícula de forma instantánea, como si estuviera en las dos a la vez y en ninguna.

             Allí donde se coloca un punto de observación, la partícula esconde su comportamiento ondulatorio como si fuera consciente de ser observada, nunca se despista y siempre acierta nuestras intenciones aunque para ello tenga que adivinar todas las trampas aleatorias que pongamos en su camino. Sí, sí, como si de verdad hubiera visitado el futuro y siempre supiera en qué momento debe sonreír a nuestra cámara como una partícula que se burla de nuestra lógica.

Esos y muchos otros son los desafíos de la materia a los que Einstein prefería buscar causas que la mecánica cuántica no reconoce. Efectivamente, ha existido una rivalidad en contra y a favor de las causas ocultas desde los comienzos de la mecánica cuántica, y cualquiera que se ha visto implicado ha tenido que adoptar una postura incondicional en esa guerra de la razón. La polémica se resume con tres conceptos que se describirán seguidamente: Entrelazamiento cuántico, localidad y realismo.

El entrelazamiento cuántico sería un efecto fantasmal si tuviera lugar a nivel macroscópico. Dos o más partículas pueden quedar ligadas de tal forma que su estudio por separado es imposible, pero lo extraño es que al separarse a grandes distancias, incluso de kilómetros, siguen compartiendo propiedades que cambian a la vez. Por ejemplo, al observar el spin en una de ellas, la otra partícula tendrá con toda seguridad el spin opuesto, lo que parece significar que el efecto de una medición se transmite de forma instantánea entre dos partículas entrelazadas.

El concepto de localidad es de origen relativista, según el cuál no existe nada más rápido que la luz. En consecuencia, los efectos de una medición local tendrán una velocidad de propagación finita y no podrán afectar al resultado de otra medición si ésta tiene lugar a distancia y en el mismo instante.

El concepto de realismo implica reconocer que los estados físicos existen antes de ser medidos, y por lo tanto existirá alguna teoría de variables ocultas que pueda explicar dichos estados. Puesto que la mecánica cuántica no puede hacer eso, debería ser una teoría incompleta. Al contrario, si la teoría de variables ocultas no existiera, la mecánica cuántica sería completa y la realidad no existiría hasta el momento de ser observada.

             Localidad y realismo fueron las razones mejor fundamentadas en contra de la mecánica cuántica. La no localidad significaba aceptar efectos fantasmales y el no realismo significaba negar la realidad física. Así era la síntesis de la paradoja EPR planteada por Albert Einstein, Boris Podolsky y Nathan Rosen, una victoria que parecía evidente, pero sin apoyo experimental hasta que los físicos John Bell y Alain Aspect diseñaron el experimento definitivo.

Al determinar los estados de una propiedad en dos partículas entrelazadas, es posible reducir el intervalo de tiempo entre las medidas de forma que la luz no tenga tiempo para recorrer la distancia entre las dos partículas. Si en esas condiciones suponemos localidad y realismo de los estados físicos, la correlación entre medidas simultáneas debería ser una prueba a favor o en contra del realismo y localidad que la teoría cuántica no reconoce.

Una teoría local podría suponer que las dos partículas ya son emitidas con estados contrarios de la propiedad a medir y su predicción coincidiría con la mecánica cuántica, pero Aspect diseñó el experimento añadiendo un factor aleatorio cuando dos fotones ya estaban en vuelo, viajando en sentidos opuestos a la velocidad de la luz. En esas condiciones una teoría local diría que era imposible la comunicación entre los fotones, y la correlación esperada con el factor aleatorio sería del 50%, pero según la mecánica cuántica sería del 70,7%. El experimento con fotones utilizaba filtros polarizadores que podían cambiar o no su dirección, y así cada fotón pasaría o sería capturado de forma independiente, siendo la coincidencia tan probable como la discrepancia (de ahí el 50% indicado antes).

Test de Bell de "dos canales"

La fuente SOURCE produce pares de fotones que son enviados en sentidos opuestos hacia un polarizador de dos canales, cuya orientación (a o b) pueda ser ajustada por el experimentador. Las señales emergentes de cada canal son detectadas y las coincidencias de cuatro tipos (++, −−, +− y −+) son contadas por el monitor de coincidencias.

¿Y qué sucedió? Pues lo que tenía que suceder, que una y otra vez los resultados fueron favorables a la mecánica cuántica, que es falso el principio de localidad con partículas entrelazadas, pero este resultado pide a gritos una interminable lista de aclaraciones en las que no es fácil ponerse de acuerdo. ¿Sucede lo mismo en escalas macroscópicas? ¿Es cierto que todo surge de un caos indeterminista y una realidad estricta no existe? ¿Es verdad que ha muerto el determinismo para siempre? ¿Hay que reconocer que la materia se crea como resultado de observaciones conscientes? ¿Y qué pasa cuando nadie observa? ¿A qué debemos llamar observador y a qué no? ¿Hay algo más rápido que la luz o lo que llamamos distancia es irreal? Si las distancias fueran una ilusión, ¿cuál sería el verdadero aspecto y naturaleza de las cosas? Si fuera cierto que la realidad surge de ondas y no de partículas, ¿qué serían esas ondas? ¿Tendríamos que hablar de algo espiritual, de otras dimensiones, o simplemente de azar probabilístico? ¿Es posible realmente que algo aparezca de la nada porque simplemente existe una posibilidad estadística, una “fluctuación cuántica”? Y esas fluctuaciones cuánticas que surgen de la nada, ¿son reales, o son la tontería soberana más grande que se haya inventado en nombre de la ciencia?

Todavía encontramos por ahí el término “decoherencia cuántica” para referirse al tránsito desde un estado indeterminista y caótico de las partículas hacia un estado coherente y razonable del mundo macroscópico. Realmente se ha intentado vender que son dos mundos desconectados, y se ha utilizado como argumento para desacreditar a todos los incautos que se han atrevido a extrapolar, utilizando la mecánica cuántica para justificar extrañas filosofías de la realidad. Pues muy bonito, a lo mejor es cierto que no faltan charlatanes aprovechados, pero también es cierto que no han faltado físicos materialistas con evidencias delante de sus narices que se niegan a reconocer. Es verdad que los fenómenos cuánticos no son fáciles de ver a escala macroscópica, pero existen, y tienen potencial más que suficiente para que sea científico investigar extrañas filosofías de la realidad.

Indeterminismo en las partículas de materia y realidad no local, son más que suficiente para decir que las cosas ya no son el resultado de sumar los efectos de cada una de sus partes, y eso es evidente por dos razones: En primer lugar porque no es lógico esperar que surja un orden de donde no lo hay, y en segundo lugar porque al hacer medidas más y más sensibles, más nos damos cuenta de que todo está entrelazado y que no hay forma de dividirlo en partes. Si el materialismo equivale a pensar que todo surge de trocitos de materia y sus conexiones (incluso la inteligencia y la consciencia humanas), entonces lo que han matado las evidencias científicas ha sido el materialismo, no la realidad.

             Son las partículas de “materia” (y sus consecuencias) las que tienen una realidad más que dudosa, pero el vacío del que todo se proyecta como gotitas de materia está repleto de variables ocultas que los físicos cuánticos no quieren reconocer. Lo llaman “ondas de probabilidad” o campo cuántico, pero lo llamen como lo llamen, es una realidad oculta, indivisible y ordenada, que se proyecta de forma temblorosa y caótica como partículas de materia. ¿Qué es entonces la materia? Yo diría que solo es la forma en que la realidad se dibuja a sí misma como finísima lluvia de puntitos localizados. Nunca es el origen de nada sino la consecuencia, y por eso no importa el indeterminismo y el caos que tanto perturba nuestra razón.

Anterior           Siguiente